A.5 Sampling Multidimensional Functions
Multidimensional sampling is also common in pbrt, most frequently when sampling points on the surfaces of shapes and sampling directions after scattering at points. This section therefore works through the derivations and implementations of algorithms for sampling in a number of useful multidimensional domains. Some of them involve separable PDFs where each dimension can be sampled independently, while others use the approach of sampling from marginal and conditional density functions that was introduced in Section 2.4.2.
A.5.1 Sampling a Unit Disk
Uniformly sampling a unit disk can be tricky because it has an incorrect intuitive solution. The wrong approach is the seemingly obvious one of sampling its polar coordinates uniformly: . Although the resulting point is both random and inside the disk, it is not uniformly distributed; it actually clumps samples near the center of the disk. Figure A.6(a) shows a plot of samples on the unit disk when this mapping was used for a set of uniform random samples . Figure A.6(b) shows uniformly distributed samples resulting from the following correct approach.
Since we would like to sample uniformly with respect to area, the PDF must be a constant. By the normalization constraint, . If we transform into polar coordinates, we have given the relationship between probability densities in Cartesian coordinates and polar coordinates that was derived in Section 2.4.1, Equation (2.22).
We can now compute the marginal and conditional densities:
The fact that is a constant should make sense because of the symmetry of the disk. Integrating and inverting to find , , , and , we can find that the correct solution to generate uniformly distributed samples on a disk is
Taking the square root of effectively pushes the samples back toward the edge of the disk, counteracting the clumping referred to earlier.
The inversion method, InvertUniformDiskPolarSample(), is straightforward and is not included here.
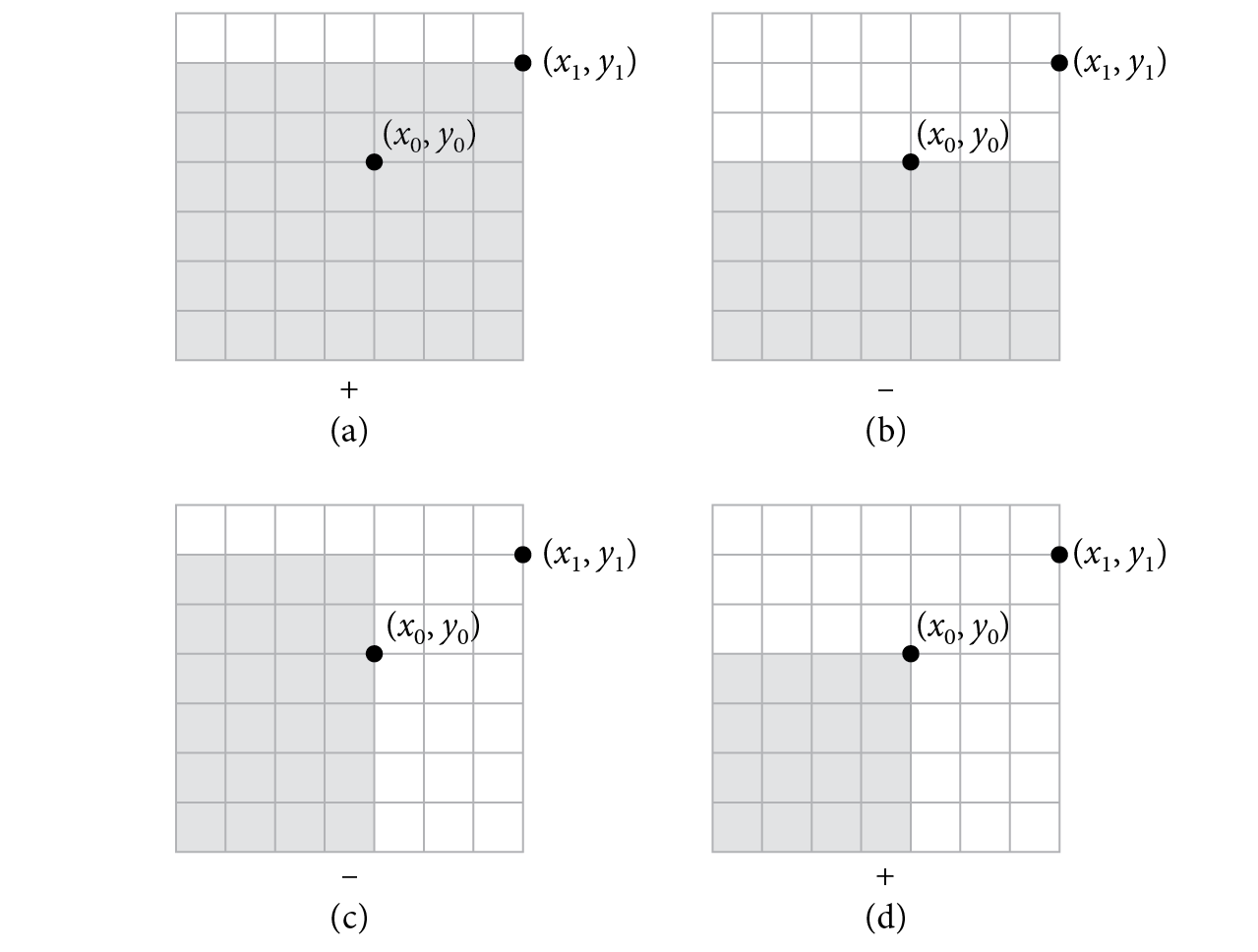
Although this mapping solves the problem at hand, it distorts areas on the disk; areas on the unit square are elongated or compressed when mapped to the disk (Figure A.7). This distortion can reduce the effectiveness of stratified sampling patterns by making the strata less compact. A better approach that avoids this problem is a “concentric” mapping from the unit square to the unit disk. The concentric mapping takes points in the square to the unit disk by uniformly mapping concentric squares to concentric circles (Figure A.8).
The mapping turns wedges of the square into slices of the disk. For example, points in the shaded area in Figure A.8 are mapped to by
See Figure A.9. The other seven wedges are handled analogously.
For the following, the random samples are mapped to the square. The point is then handled specially so that the following code does not need to avoid dividing by zero.
All the other points are transformed using the mapping from square wedges to disk slices by way of computing polar coordinates for them. The following implementation is carefully crafted so that the mapping is continuous across adjacent slices.
The corresponding inversion function, InvertUniformDiskConcentricSample(), is not included in the text here.
A.5.2 Uniformly Sampling Hemispheres and Spheres
The area of a unit hemisphere is , and thus the PDF for uniform sampling must be .
We will use spherical coordinates to derive a sampling algorithm. Using Equation (2.23) from Section 2.4.1, we have . This density function is separable. Because ranges from 0 to and must have a constant PDF, and therefore . The two CDFs follow:
Inverting these functions is straightforward, and in this case we can tidy the result by replacing with , giving
Converting back to Cartesian coordinates, we get the final sampling formulae:
This sampling strategy is implemented in the following code. Two uniform random numbers are provided in u, and a vector on the hemisphere is returned.
For each PDF evaluation function, it is important to be clear which PDF is being evaluated—for example, we have already seen directional probabilities expressed both in terms of solid angle and in terms of . For hemispheres (and all other directional sampling in pbrt), these functions return probability with respect to solid angle. Thus, the uniform hemisphere PDF function is trivial and does not require that the direction be passed to it.
The inverse sampling method can be derived starting from Equation (A.17).
Sampling the full sphere uniformly over its area follows almost exactly the same derivation, which we omit here. The end result is
The PDF is , one over the surface area of the unit sphere.
The sampling inversion method also follows directly.
A.5.3 Cosine-Weighted Hemisphere Sampling
As we saw in the discussion of importance sampling (Section 2.2.2), it is often useful to sample from a distribution that has a shape similar to that of the integrand being estimated. Many light transport integrals include a cosine factor, and therefore it is useful to have a method that generates directions according to a cosine-weighted distribution on the hemisphere. Such a method gives samples that are more likely to be close to the top of the hemisphere, where the cosine term has a large value, rather than near the bottom, where the cosine term is small.
Mathematically, this means that we would like to sample directions from a PDF
Normalizing as usual,
Thus,
We could compute the marginal and conditional densities as before, but instead we can use a technique known as Malley’s method to generate these cosine-weighted points. The idea behind Malley’s method is that if we choose points uniformly from the unit disk and then generate directions by projecting the points on the disk up to the hemisphere above it, the result will have a cosine-weighted distribution of directions (Figure A.10).
Why does this work? Let be the polar coordinates of the point chosen on the disk (note that we are using instead of the usual for the polar angle here). From Section A.5.1, we know that the joint density gives the density of a point sampled on the disk.
Now, we map this point to the hemisphere. The vertical projection gives , which is easily seen from Figure A.10. To complete the transformation, we need the determinant of the Jacobian
Therefore,
which is exactly what we wanted! We have used the transformation method to prove that Malley’s method generates directions with a cosine-weighted distribution. Note that this technique works with any uniform disk sampling approach, so we can use the earlier concentric mapping just as well as the simpler method.
Because directional PDFs in pbrt are defined with respect to solid angle, the PDF function returns the value .
Finally, a directional sample can be inverted purely from its coordinates on the disk.
A.5.4 Sampling Within a Cone
It is sometimes useful to be able to uniformly sample rays in a cone of directions. This distribution is separable in , with , and so we therefore need to derive a method to sample a direction up to the maximum angle of the cone, . Incorporating the term from the measure on the unit sphere from Equation (4.8), we have
So and .
The PDF can be integrated to find the CDF and the sampling technique for follows:
The following code samples a canonical cone around the axis; the sample can be transformed to cones with other orientations using the Frame class.
The inversion function, InvertUniformConeSample(), is not included here.
A.5.5 Piecewise-Constant 2D Distributions
Building on the approach for sampling piecewise-constant 1D distributions in Section A.4.7, we can apply the marginal-conditional approach to sample from piecewise-constant 2D distributions. We will consider the case of a 2D function defined over a user-specified domain by a 2D array of sample values. This case is particularly useful for generating samples from distributions defined by image maps and environment maps.
Consider a 2D function defined by a set of values where , , and gives the constant value of over the range . Given continuous values , we will use to denote the corresponding discrete indices, with and so that .
Integrals of are sums of , so that, for example, the integral of over the domain is
Using the definition of the PDF and the integral of , we can find ’s PDF,
Because this function only depends on , it is thus itself a piecewise-constant 1D function, , defined by values. The 1D sampling machinery from Section A.4.7 can be applied to sampling from its distribution.
Given a sample, the conditional density is then
Note that, given a particular value of , is a piecewise-constant 1D function of that can be sampled with the usual 1D approach. There are such distinct 1D conditional densities, one for each possible value of .
Putting this all together, the PiecewiseConstant2D class provides functionality similar to PiecewiseConstant1D, except that it generates samples from piecewise-constant 2D distributions.
Its constructor has two tasks. First, it computes a 1D conditional sampling density for each of the individual values using Equation (A.17). It then computes the marginal sampling density with Equation (A.17). (PiecewiseConstant2D provides a variety of additional constructors, not included here, including ones that take an Array2D to specify the values. See the pbrt source code for details.)
PiecewiseConstant1D can directly compute the distributions from each of the rows of function values, since they are laid out linearly in memory. The and terms from Equation (A.17) do not need to be included in the values passed to PiecewiseConstant1D since they have the same value for all the values and are thus just a constant scale that does not affect the normalized distribution that PiecewiseConstant1D computes.
Given the conditional densities for each value, we can find the 1D marginal density for sampling each one, . Because the PiecewiseConstant1D class has a method that provides the integral of its function, it is just necessary to copy these values to the marginalFunc buffer so they are stored linearly in memory for the PiecewiseConstant1D constructor.
The integral of the function over the domain is made available via the Integral() method. Because the marginal distribution is the integral of one dimension, its integral gives the function’s full integral.
As described previously, in order to sample from the 2D distribution, first a sample is drawn from the marginal distribution in order to find the coordinate of the sample. The offset of the sampled function value gives the integer value that determines which of the precomputed conditional distributions should be used for sampling the value. Figure A.11 illustrates this idea using a low-resolution image as an example.
The value of the PDF for a given sample value is computed as the product of the conditional and marginal PDFs for sampling it.
The Invert() method, not included here, inverts the provided sample by inverting the sample using the marginal distribution and then inverting via the appropriate conditional distribution.
A.5.6 Windowed Piecewise-Constant 2D Distributions
WindowedPiecewiseConstant2D generalizes the PiecewiseConstant2D class to allow the caller to specify a window that limits the sampling domain to a given rectangular subset of it. (This capability was key for the implementation of the PortalImageInfiniteLight in Section 12.5.3.) Before going into its implementation, we will start with the SummedAreaTable class, which provides some capabilities that make it easier to implement. We have encapsulated them in a stand-alone class, as they can be useful in other settings as well.
In 2D, a summed-area table is a 2D array where each element stores a sum of values from another array :
where here we have used C++’s zero-based array indexing convention.
Summed-area tables can be used to compute the sum of array values over rectangular regions of the original array in constant time. If the array is interpreted as samples of a function, a summed-area table can efficiently compute integrals over arbitrary rectangular regions in a similar fashion. (Summed-area tables are therefore sometimes referred to as integral images.) They have a straightforward generalization to higher dimensions, though two of them suffice for pbrt’s needs.
The constructor takes a 2D array of values that are used to initialize its sum array, which holds the corresponding sums. The first entry is easy: it is just the entry from the provided values array.
All the remaining entries in sum can be computed incrementally. It is easiest to start out by computing sums as varies with and vice versa.
The remainder of the sums are computed incrementally by adding the corresponding value from the provided array to two of the previous sums and subtracting a third. It is possible to use the definition from Equation (A.17) to verify that this expression gives the desired value, but it can also be understood geometrically; see Figure A.12.
We will find it useful to be able to treat the sum as a continuous function defined over . In doing so, our implementation effectively treats the originally provided array of values as the specification of a piecewise-constant function. Under this interpretation, the stored sum values effectively represent the function’s value at the upper corners of the box-shaped regions that the domain has been discretized into. (See Figure A.13.)
This Lookup() method returns the interpolated sum at the given continuous coordinate values.
It is more convenient to work with coordinates that are with respect to the array’s dimensions and so this method starts by scaling the provided coordinates accordingly. Note that an offset of is not included in this remapping, as is done when indexing pixel values (recall the discussion of this topic in Section 8.1.4); this is due to the fact that sum defines function values at the upper corners of the discretized regions rather than at their center.
Bilinear interpolation of the four values surrounding the lookup point proceeds as usual, using LookupInt() to look up values of the sum at provided integer coordinates.
LookupInt() returns the value of the sum for provided integer coordinates. In particular, it is responsible for handling the details related to the sum array storing the sum at the upper corners of the domain strata.
If either coordinate is zero-valued, the lookup point is along one of the lower edges of the domain (or is at the origin). In this case, a sum value of 0 is returned.
Otherwise, one is subtracted from each coordinate so that indexing into the sum array accounts for the zero sums at the lower edges not being stored in sum.
Summed-area tables compute sums and integrals over arbitrary rectangular regions in a similar way to how the interior sum values were originally initialized. Here it is also possible to verify this computation algebraically, but the geometric interpretation may be more intuitive; see Figure A.14.
The SummedAreaTable class provides this capability through its Integral() method, which returns the integral of the piecewise-constant function over a 2D bounding box. Here, the sum of function values over the region is converted to an integral by dividing by the size of the function strata over the domain. We have used double precision here to compute the final sum in order to improve its accuracy: especially if there are thousands of values in each dimension, the sums may have large magnitudes and thus taking their differences can lead to catastrophic cancellation.
Given SummedAreaTable’s capability of efficiently evaluating integrals over rectangular regions of a piecewise-constant function’s domain, the WindowedPiecewiseConstant2D class is able to provide sampling and PDF evaluation functions that operate over arbitrary caller-specified regions.
The constructor both copies the provided function values and initializes a summed-area table with them.
With the SummedAreaTable in hand, it is now possible to bring the pieces together to implement the Sample() method. Because it is possible that there is no valid sample inside the specified bounds (e.g., if the function’s value is zero), an optional return value is used in order to be able to indicate such cases.
The first step is to check whether the function’s integral is zero over the specified bounds. This may happen due to a degenerate Bounds2f or due to a plain old zero-valued function over the corresponding part of its domain. In this case, it is not possible to return a valid sample.
As discussed in Section 2.4.2, multidimensional distributions can be sampled by first integrating out all of the dimensions but one, sampling the resulting function, and then using that sample value in sampling the corresponding conditional distribution. WindowedPiecewiseConstant2D applies that very same idea, taking advantage of the fact that the summed-area table can efficiently evaluate the necessary integrals as needed.
For a 2D continuous function defined over a rectangular domain from to , the marginal distribution in is defined by
and the marginal’s cumulative distribution is
The integrals in both the numerator and denominator of can be evaluated using a summed-area table. The following lambda function evaluates , using a cached normalization factor for the denominator in bInt to improve performance, as it will be necessary to repeatedly evaluate Px in order to sample from the distribution.
Sampling is performed using a separate utility method, SampleBisection(), that will also be useful for sampling the conditional density in .
SampleBisection() draws a sample from the density described by the provided CDF P by applying the bisection method to solve for over a specified range . (It expects to have the value 0 at min and 1 at max.) This function has the built-in assumption that the CDF is piecewise-linear over equal-sized segments over . This fits SummedAreaTable perfectly, though it means that SampleBisection() would need modification to be used in other contexts.
The initial min and max values bracket the solution. Therefore, bisection can proceed by successively evaluating at their midpoint and then updating one or the other of them to maintain the bracket. This process continues until both endpoints lie inside one of the function discretization strata of width .
Once both endpoints are in the same stratum, it is possible to take advantage of the fact that is known to be piecewise-linear and to find the value of in closed form.
Given the sample , we now need to draw a sample from the conditional distribution
which has CDF
Although the SummedAreaTable class does not provide the capability to evaluate 1D integrals directly, because the function is piecewise-constant we can equivalently evaluate a 2D integral where the range spans only the stratum of the sampled value.
bCond stores the bounding box that spans the range of potential values and the stratum of the sample. It is necessary to check for a zero function integral over these bounds: this should not be possible mathematically, but may be the case due to floating-point round-off error. In that rare case, conditional sampling is not possible and an invalid sample must be returned.
Similar to the marginal CDF , we can define a lambda function to evaluate the conditional CDF . Again precomputing the normalization factor is worthwhile, as Py will be evaluated multiple times in the course of the sampling operation.
The PDF value is computed by evaluating the function at the sampled point p and normalizing with its integral over b, which is already available in bInt.
The Eval() method wraps up the details of looking up the function value corresponding to the provided 2D point.
The PDF method implements the same computation that is used to compute the PDF in the Sample() method.